Statistical Inference 课后小结 | Thinking in Crowd / 鹄思乱想

Contents

好不容易才把 Statistical Inference 的课上完, 真是有点吃力. 简略把教的东西列出来吧, 方便日后再复习.

概率

条件概率 (Conditional Probability)

当 B 发生的概率为 P(B) 时, A 发生的概率为 P(A|B) = P(A ∩ B) / P(B).
如果 A 和 B 是完全独立的事件, 那么 P(A|B) = P(A)P(B) / P(B) = P(A).

Bayes’ rule

P(B|A) = P(A|B)P(B) / (P(A|B)P(B) + P(A|B𝑐)P(B𝑐))

P(B𝑐) = 1 - P(B)

诊断测试 (Diagnostic test)

首先, 诊断测试里面有几个定义先要搞清楚：

+ 测试为患病的情况
- 测试为没有患病的情况
D 确定患病的情况
D𝑐 确定没有患病的情况
sensitivity 当确实患病时, 测试为患病的概率 P(+ | D)
specificity 当确实没有患病时, 测试为没有患病的概率 P(- | D𝑐)
positive predictive value P(D | +)
negative predictive value P(D𝑐 | -)
prevalance of the disease P(D)

有个很有趣的例子：
假如在一项 HIV 的研究中, 有一种 HIV 抗体检查的 sensitivity 是 99.7%, specificity 是 98.5%. (看起来这个抗体检查应该很准, 对吧？) 如果一个人, 从 0.1% prevalence HIV 的群体中抽出来, 他做了这个抗体检查后, 结果是阳性也就是检查结果显示他应该有 HIV. 那么, 你觉得他确实患病的概率有多高呢？

那我们来看看 positive predictive value 也就是 P(D | +) 概率是多少. 用 Bayes’ rule 公式代入去算一下可得 0.062. 不是很高吧？这么低的数值是由于低 prevalence 造成的。但是如果说你知道那个人是有用毒品习惯, 并且和 HIV 人士有接触。你会不会觉得他患病的概率更高？其实影响的因素 prevalence 一点没变, 可是我们对所谓证据的诠释不同了.

Likelihood ratios

DLR+, diagnostic likeihood ratio of a positive test, is P(+ | D) / P(+ | D𝑐)

`sensitivity / (1 - specificity)`

DLR-, diagnostic likeihood ratio of a negative test, is P(- | D) / P(- | D𝑐)

`(1 - sensitivity) / specificity`

根据 Bayes’ rule 可以推导出：

P(D | +) / P(D𝑐 | +) = DLR+ * P(D) / P(D𝑐)

post-test odds of D = DLR+ * pre-test odds of D (odds: 一个概率除以 1 减去它)

相同道理： P(D | -) / P(D𝑐 | -) = DLR- * P(D) / P(D𝑐)

IID

Independent: statistically unrelated from one and another
Identically distributed: all having been drawn from the same population distribution

期望值 (Expected Value)

Mean: 分布的中值特征
Variance 和 Standard Deviation: 分布性的特征 (How spread out)

Sample expected values 是用来推测 population 的特征的。

E[X] = ∑ xp(x) 表示了数据分布的位置和权重的中值。比如, 丟硬币:

E[X] = 0 * 0.5 + 1 * 0.5 = 0.5

如果说硬币正反不是概率均等, 而是正面的概率为 p, 那 E[X] = 0 * (1 - p) + 1 * p = p

同理掷骰子, 数字面值的中值, 那就是 E[X] = 1 * 1/6 + 2 * 1/6 + ... + 6 * 1/6 = 3.5

Mean

通过取样, 来获取中值, 这个中值本身, 其实也是随机变量, 它的分布也是有个中值的。这个中值, 如果和它原来要推导的中值本身是一致的, 我们就会说这个推导是公正的 (unbiased)。

这个说法有点拗口, 其实是这样的是. 比如说, 丟硬币本身的中值是 0.5. 那么, 我们有两种做法：

一种是丢一次硬币, 记录下一次 0 或者 1, 重复丢 n 次, 然后算它本身的中值就是 0.5. 无限下去的理论值就是 population mean.
另一种就是丢 m 次硬币, 先算一次中值 (sample mean), 记录下这个中值, 再重复丢 n 次, 最后再算一次中值. 其实也就是中值的中值.

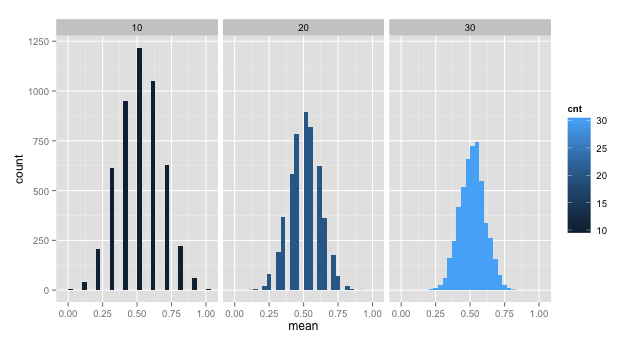
中值的中值 如果说和 population mean 是一致的, 那这个推导就是公正的了. 而且, 如果算 sample mean 的数据 (上面的 m) 越多, 那么中值分布的质量函数 (density / mass function) 最越集中在 population mean.

GetSampleMean <- function(count) {
  data.frame(mean = replicate(5000, mean(sample(c(0, 1), count, replace = T))), cnt = count)
}

data.df <- rbind(GetSampleMean(10), GetSampleMean(20), GetSampleMean(30))

library(ggplot2)
qplot(x = mean, data = data.df, facets = . ~ cnt, fill = cnt)

方差 (Variance)

随机变量到中值的距离 Var(X) = E[(X - μ)2] = E[X²] - E[X]²

假如一个硬币正面的概率是 p. 那它的 Variance 就是:

1
2
3

E[X] = 0 * (1 - p) + 1 * p = p
E[X²] = E[X] = p
Var(X) = E[X²] - E[X]² = p - p² = p(1 - p)

标准差 (Standard Deviation): Variance 的平方根, S
标准误 (Standard Error): S/√n

同中值一样, 样本的 Variance, S², 也是随机变量, 它的分布也是集中在 population variance, σ².

常见的概率分布模型

伯努利分布 (Bernoulli distribution)

又名两点分布或者 0-1 分布. 通常定 1 值的概率为 p, 0 值的概率为 (1 - p). 它的中值为 p, 方差为 p(1 - p).

伯努利試驗 (Binomial trial)

这个试验的随机变量，其实是伯努利分布随机值的总和 X = ∑ⁿXᵢ, Xᵢ 为 Bernoulli(p).

它的质量函数 (mass function) 是: P(X = x) = (n x) * pˣ * (1 - p)ⁿ⁻ˣ. (n x) 是从 n 中取 x 的组合数.

举个例子说，如果一个家庭有 8 个孩子, 7 个是女的，没有孪生. 如果生男生女的概率为 0.5, 那么 8 个孩子中，生 7 个或以上的女孩概率是多大?

(8 7) * 0.5⁷ * (1 - 0.5)¹ + (8 8) * 0.5⁸ * (1 - 0.5)⁰ ≈ 0.04

对应的 R 代码为:

1
2
3

choose(8, 7) * 0.5^8 + choose(8, 8) * 0.5^8

pbinom(6, size = 8, prob = 0.5, lower.tail = FALSE)

正态分布 (Normal distribution)

如果它的中值是 μ, 方差是 σ², 它的表达式可以写成 X ~ N(μ, σ²). 如果 μ = 0, σ² = 1, 它就是标准正态分布, 通常用 Z 来表示.

如果一个随机分布是正态分布 X ~ N(μ, σ²), 那么经过 (X - μ) / σ 转换后的随机变量就会是标准正态分布.
反过来，如果 Z 是标准正态分布, X = μ + σZ ~ N(μ, σ²).

正态分布的特性

68%, 95%, 99% 的正态质量在 1, 2, 3 的标准差内.
-1.28， -1.645， -1.96， -2.33 分别是标准正态分布的 10th, 5th, 2.5th, 1st 区域
由于对称性, 1.28， 1.645， 1.96， 2.33 分别是标准正态分布的 90th, 95th, 97.5th, 99th 区域

比如说 N(μ, σ²) 分布的 95th percentile 是多少?

μ + σ * 1.645 或者

1	qnorm(.95, mean = μ, sd = σ)`

再举个例. 如果一个网面的点击数平均值在 1020, 标准差在 50, 那么点击数超过 1160 的概率是多少?

1	pnorm(1160, mean = 1120, sd = 50, lower.tail = F)

(Poisson distribution)

它的中值和方差都是 λ. 可用于对 counts, event-time or survival data, contingency table 进行建模.
当随机变量的 n 很大，概率 p 很小的时候，Poisson 的分布可以用于近似于 Binomial 分布.

当它用来对速率的随机变量建模时:

X ~ Poisson(λt)

λ = E[X/t] 表示在单位时间内的数量
t 是总时间

比如说人出现在公交站的数量是 Poisson 分布. 假如每小时 2.5 个人, 如果我们观察 4 个小时, 3 个或者少于 3 个人的概率是多大?

1	ppois(3, lambda = 2.5 * 4)

渐近 (Asymptotics)

大数定律 (Law of Large Number)

对于 IID 的随机值来说, 只要取的样本足够多, 它的平均值, 最终会和理论的 population mean 是一致的.

中心极限定理 (Central Limit Theorem)

对于 IID 的随机值来说, 只要取的样本足够多, 它的平均值的分布会呈现出正态分布.

样本 Xₙ 可以说是基本呈现出为 N(μ, σ²/n) 的正态分布.

Confidence Intervals

对于正态分布来说，随机值 X 大于 μ + 2σ/√n 或者小于 μ - 2σ/√n 的概率只有 5%. 那么 X ± 2σ/√n 就叫做 μ 的 95% 区间.

Est ± ZQ * SE

T Confidence Intervals

Est ± TQ * SE

一般如果要进行分组之间的数据比较，会把分级之间的数据差，做 t interval 分析.

比如 R 里面的 Sleep data, 分别比较两组不同的药物，对人的睡眠质量的影响.

data(sleep)
head(sleep)

##   extra group ID
## 1   0.7     1  1
## 2  -1.6     1  2
## 3  -0.2     1  3
## 4  -1.2     1  4
## 5  -0.1     1  5
## 6   3.4     1  6

g1 <- sleep$extra[1 : 10]
g2 <- sleep$extra[11 : 20]
difference <- g2 - g1
mn <- mean(difference)
s <- sd(difference)
n <- 10

mn + c(-1, 1) * qt(.975, n-1) * s / sqrt(n)
t.test(difference)
t.test(g2, g1, paired = TRUE)

##        [,1] [,2]
## [1,] 0.7001 2.46
## [2,] 0.7001 2.46

上面的比较是把数据认为是 paired = TRUE 的.

那如果是独立分组的数据的 t interval (恒定标准差的情况下) 怎么计算呢?
假如我们要计算 μᵧ - μₓ 的 (1 - α) * 100% 信心区间,

Y - X ± tₙₓ₊ₙᵧ₋₂ * Sₚ * ( 1 / nₓ + 1 / nᵧ)^0.5

Sₚ² = {(nₓ - 1) * Sₓ² + (nᵧ - 1) * Sᵧ²} / (nₓ + nᵧ - 2)

下面的比较是把数据认为是 paired = FALSE 的.

sp <- sqrt( ((n1 - 1) * sd(x1)^2 + (n2-1) * sd(x2)^2) / (n1 + n2-2))
semd <- sp*sqrt(1/n1+1/n2)

md + c(-1,1) * qt(.975,n1+n2-2) * semd
t.test(g2, g1, paired = FALSE, var.equal = TRUE)$conf

##         [,1]  [,2]
## [1,] -0.2039 3.364
## [2,] -0.2039 3.364

可见两次的结果是非常不同的. 那到底怎么决定数据是否是 pair, 是否是独立的呢？

比如说, 如果我们要检测非吸烟者和吸烟者的 BMI 指数, 因为这两组人群是完全不同的, 所以就是独立的.
或者说如果测试完全分开的两组一员, 一组使用药物, 一组使用安慰剂来测试药物的效用, 这也是独立的.

但如果说测试是同一组人员, 使用药物前后的比较, 那就应该是 paired.

那如果是独立分组的数据的 t interval (非恒定标准差的情况下) 怎么计算呢?

Y - X ± tdf * ( Sₓ² / nₓ + Sᵧ² / nᵧ)^0.5

tdf 里面的 degree of freedom 的计算为:

df = ( Sₓ² / nₓ + Sᵧ² / nᵧ)² / {(Sₓ² / nₓ)² / (nₓ - 1) + (Sᵧ² / nᵧ)² / (nᵧ - 1)}

参考链接: http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_Confidence_Intervals/BS704_Confidence_Intervals.html

Hypothesis testing

定义

H₀, H-nought, 通常代表 “没有关联”, “没有影响” 的观点，又称为零假设. 它是目前要测试和证明的假设, 通常先被假定为正确的, 然后希望用统计数据来证明为错误或者需要慎重考虑的假设.

Hₐ, (alternative hypothesis) 就是对应的希望被证明为正确的假设.

比如说, Centers for Disease Control (CDC) 报道了从 1960 到 2002 年的身高体重质量指数趋势. 报告认为美国人在 2002 年比 1960 年重了很多, 而只是高了一点; 无论男女平均大约增加 24 磅. 在 2002 年, 男性平均体重为 191 磅. 假定有调查者认为到 2006 年, 也就是说男性平均体重将多于 191 磅. 那我们就可以把体重没有变化的推测定义为 H₀.

Null Hypothesis      H₀: μ = 191         (没变化)
Research Hypothesis  Hₐ: μ > 191         (调查人员的假定推测)

为了验证这个假定, 我们在 2006 年随机选定了一组美国男性来测量体重. 如果我们抽取的样本为 n = 100 人, 测量结果为: X = 197.1, s = 25.6:

P(X > 197.1) = P(Z > (197.1 - 191) / (25.6 / √100)) = P(Z > 2.38) = 1 - 0.9913 = 0.0087

也就是说, 如果说体重没有变化, 取样得到平均値为 197.1 的可能性还不到 1%. 那我们说 H₀ 是否成立呢?

样例取自: http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_HypothesisTest-Means-Proportions/

错误类型

Type I Error: 当事实为 H₀ 时，我们推测出的结果为 Hₐ
Type II Error: 当事实为 Hₐ 时，我们推测出的结果为 H₀

现在我们尝试把场景应用到法律当中, H₀ 为被控方是无罪的. 那么我们就需要找到一个标准来断定他是有罪的 (Reject H₀). 假如标准太高, 把无罪的人错误定罪的可能性就变高了 (Type I Error). 相反标准低了, Type II Error 就高了.

所以, 其中一种做法就是选出一个常量 C (Critical Value), 使得样本的平均值 X 比它大时, 我们可以 Reject H₀. 要得到这个 C, 我们先要定出 α (level of significance), 来表示说如果在 H₀ 为真的时候, 我们却 Reject 了它的可能性, 也就是 Type I Error P(X > C; H₀) = 5%.

Upper, Lower, and Two Failed Test

一般来说, 对应 H₀, Hₐ 有下面三种形式:

H₁ : μ < μ₀
H₂ : μ ≠ μ₀
H₃ : μ > μ₀

所以, 如果说 TS (Test Statistic) = (X - μ) / (s/√n) 的话, 以下的情况就分别可以 Reject H₀:

 TS  ≤ Zₐ
|TS| ≥ Z₁₋ₐ∕₂
 TS  ≥ Z₁₋ₐ

和 Confidence Interval 的关系

对于 μ 来说, (1 - α) * 100% 的 confidence interval 范围内的所有的值, 都无法 (Failed to) Reject H₀.

P-values

P-value 就是在 H₀ 的前提下, 观测到的样本值出现的可能性. 如果这个可能性很少, 要么 H₀ 为真, 并且我们观测到的值很极端, 要么 H₀ 为假.

P-value 和 α (level of significance) 是不同的. P-value 只是简单描述了在 H₀ 情况下, 某值出现的可能性. α 则是我们选定的用来判定是否 Reject H₀ 的标准. 当 P-value 小于 α 的时候，我们就可以 Reject H₀.

two sided hypothesis test, double the smaller of the two “one sided hypothesis test P-values”.

比如下面一个例子:

有 18 位肥胖人士, 随机抽取 9 位服用新的减肥药, 9 位服用安慰剂. 4 星期后测量的 BMI 指数的平均变化为, 服用减肥药的为 -3kg/m2, 服用安慰剂的为 1kg/m2. 两组人员的标准差为 1.5kg/m2 和 1.8kg/m2. 那么现在的 BMI 变化对使不使用减肥药有区别吗? 假定数据是正态的, 并且 population variance 是相同的, 尝试给出 two sided t test 的 P-value.

n1 <- n2 <- 9
x1 <- -3  ## treated
x2 <- 1  ## placebo
s1 <- 1.5  ## treated
s2 <- 1.8  ## placebo
s <- sqrt(((n1 - 1) * s1^2 + (n2 - 1) * s2^2)/(n1 + n2 - 2))  # 恒定标准差, 独立分组的数据
ts <- (x1 - x2) / (s * sqrt(1/n1 + 1/n2))  # Test statistic
2 * pt(ts, n1 + n2 - 2)

Power

当事实为 Hₐ 时, 我们推测出的结果为 Hₐ 的可能性 (sensitivity).

Power = 1 - β (Type II error rate)

假如我们要推测的 Hₐ 为 μ > μ₀:

Power = P((X - μ₀) / (σ/√n) > z₁₋ₐ | μ = μₐ) # 当 μₐ 趋近 μ₀ 时, Power 趋近 α
= P((X - μₐ + μₐ - μ₀) / (σ/√n) > z₁₋ₐ | μ = μₐ)
= P((X - μₐ) / (σ/√n) > z₁₋ₐ - (μₐ - μ₀) / (σ/√n) | μ = μₐ)
= P(Z > z₁₋ₐ - (μₐ - μ₀) / (σ/√n) | μ = μₐ)
= P(Z > zβ)

z₁₋ₐ 为标准正态分布在 α 的区域值如 1.645 (5%)

假定在 H₀:μ = μ₀ 的情况下, 统计数据为 N(0, 1) 的正态分布, 那么在 Hₐ:μ = μₐ 的情况下, 统计数据就为 N((μₐ - μ₀) / (σ/√n), 1) 的正态分布. 所以，也可以通过 pnorm(1.645, mean = (μₐ - μ₀) / (σ/√n), sd = 1, lower.tail = F) 来计算出 Power.

根据上面的推理, 我们还可以得出一个等式: z₁₋ₐ - (μₐ - μ₀) / (σ/√n) = zβ.
也就是说 Power 和 (μₐ - μ₀) / (σ/√n) 的比值相关. (μₐ - μ₀) / σ 为 effect size.

Multiple testing

Types of Error

              β = 0   β ≠ 0   Hypotheses
Claim β = 0   U       T       m - R
Claim β ≠ 0   V       S       R
Claims        m₀      m - m₀  m

m - total number of hypotheses tested
m₀ - number of true H₀
m - m₀ - number of true Hₐ
V - number of false positive (Type I error / false discoveries)
S - number of true positive (true discoveries)
T - number of false negative (Type II error)
U - number of true negative
R - number of rejected H₀

Error Rates

False positive rate - The rate at which false results (β = 0) are called significant: E[V/m₀]
Family wise error rate (FWER) - The probability of at least one false positive Pr(V ≥ 1)
False discovery rate (FDR) - The rate at which claims of significance are false E[V/R]

Correction

Controlling FWER - Bonferroni correction

假定做 m 次测试, 要把 FWER 控制在 α, 也就是 Pr(V ≥ 1) < α.
然后把新的 α 设置为 α / m, 所有小于这个新的 α 的 P-value 就是 significant 的.
这种方法的优点就是容易计算, 缺点就是得出的值会非常保守.

Controlling FDR

假定做 m 次测试, 要把 FDR 控制在 α, 也就是 E[V/R].
把 P-value 从小到大排好序 P(1), …, P(m), 任何 P(i) ≤ α * i/m 都是 significant 的.
这种方法的优点就是相对容易计算, 没那么保守, 缺点就是 false positive 可能性增加, 而且关联数据可能表现诡异.

Adjusted P-values

注意, 修正过的就已经不能算是 P-values 了.
假定我们有 P(1), …, P(m), 我们可以把每一个 P-values * m, 最大值为 1. 如果得出来的值小于 α, 那就是在 Control FWER 上是 significant 的.

Resampled inference

不断的从已有数据集中取数据出来创造新的数据集. R 里面有两个很有用的工具:

jackknife

原理是从一组数据中每次删除一个值, 然后用剩下的 (n - 1) 个数据来计算推测要推导的结论. 所以也就是说会有 n 种数据组合和 n 次推导值. 这种做法通常会用在推算偏差和标准误上面. 像中值 (mean) 这种 unbiased 的数据是不用 jackknife 来做的.

计算过程是这样的:

X₁, …, Xₙ 是一组测量数据值
假定 θ 是用以上数据全集推导出来的值 (比如 median)
θᵢ 是把 Xᵢ 删除后推导出来的值
假定 θbar = 1/n * ∑ⁿθᵢ

jackknife 算出来的偏差就是 (n - 1) * (θbar - θ), 标准误就是 [(n - 1)/n * ∑ⁿ(θᵢ - θbar)²] ^ 0.5

bootstrap

bootstrap 是 non-parametric 的. 通常用于 confidence internal 和标准误上面. bootstrap 原则是指 using the distribution defined by the data to approximate its sampling distribution.

实际操作上来说, bootstrap 原则都是通过模拟来的执行的. 一般都是不断的从观测的数据中取样计算分布状况, 来模拟完整的数据集的分布.
从多次的模拟计算中得到的统计概率去计算 confidence interval 或者标准误.

library(UsingR)
library(bootstrap)
data(father.son)

x <- father.son$sheight
n <- length(x)
B <- 1000

resamples <- matrix(sample(x, n * B, replace = TRUE), B, n)
medians <- apply(resamples, 1, median)
sd(medians)
## [1] 0.08452927

quantile(medians, c(0.025, 0.975))
##     2.5%    97.5%
## 68.44474 68.81588